Table Of Content

Randomly dividing the subjects into the 2 groups is the most likely to make the treatment and control groups as alike as possible because it eliminates human bias. Not only differences that the researcher has identified as relevant, but on all characteristics, including the hidden ones that the researcher might not realize are important. The design is balanced having the effect that our usual estimators andsums of squares are “working.” In R, we would use the model formulay ~ Block1 + Block2 + Treat.
Allocate your observations into treatments
For each experiment, identify (1) which experimental design was used; and (2) why the researcher might have used that design. Here are the main steps you need to take in order to implement blocking in your experimental design. Imagine an extreme scenario where all of the athletes that are running on turf fields get allocated into one group and all of the athletes that are running on grass fields are allocated into the other group. In this case it would be near impossible to separate the impact that the type of cleats has on the run times from the impact that the type of field has. Note that the least squares means for treatments when using PROC Mixed, correspond to the combined intra- and inter-block estimates of the treatment effects. Since the first three columns contain some pairs more than once, let's try columns 1, 2, and now we need a third...how about the fourth column.
Identify nuisance variables
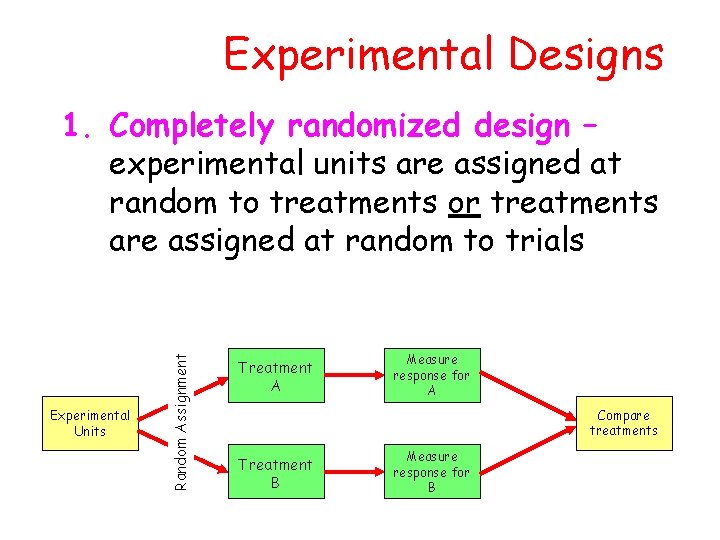
When all treatments appear at least once in each block, we have a completely randomized block design. When we have a single blocking factor available for our experiment we will try to utilize a randomized complete block design (RCBD). We also consider extensions when more than a single blocking factor exists which takes us to Latin Squares and their generalizations.
3 Paired Analysis
The single design we looked at so far is the completely randomized design (CRD) where we only have a single factor. In the CRD setting we simply randomly assign the treatments to the available experimental units in our experiment. If we choose one of the RCB Design Structures, Temperature effects are completely randomized at the Run level. Recipe is nested within temperature and has a different error structure than temperature, because each dough appears within each run.
Why is the randomized controlled double-blind experiment ideal?
Experimental research of concrete floor blocks with crushed bricks and tiles aggregate - ScienceDirect.com
Experimental research of concrete floor blocks with crushed bricks and tiles aggregate.
Posted: Mon, 25 Dec 2017 14:02:49 GMT [source]
Therefore, it would be very useful to block on gender in order to remove its effect as an alternative explanation of the outcome. And because physical capability differs substantially between males and females, the authors decided to block on gender. So in both experiments we need to do six mass spectrometry runs. We can create a (random) Latin Square design in R for example with thefunction design.lsd of the package agricolae (de Mendiburu 2020). Connect and share knowledge within a single location that is structured and easy to search.
7 - Incomplete Block Designs
A farmer possesses five plots of land where he wishes to cultivate corn. He wants to run an experiment since he has two kinds of corn and two types of fertilizer. Moreover, he knows that his plots are quite heterogeneous regarding sunshine, and therefore a systematic error could arise if sunshine does indeed facilitate corn cultivation. Minitab’s General Linear Command handles random factors appropriately as long as you are careful to select which factors are fixed and which are random. Condition one attempted to recall a list of words that were organized into meaningful categories; condition two attempted to recall the same words, randomly grouped on the page. Although order effects occur for each participant, they balance each other out in the results because they occur equally in both groups.
What is blocking in experimental design?
We could put individuals into one of two blocks (male or female). And within each of the two blocks, we can randomly assign the patients to either the diet pill (treatment) or placebo pill (control). By blocking on sex, this source of variability is controlled, therefore, leading to greater interpretation of how the diet pills affect weight loss. Experimental design refers to how participants are allocated to different groups in an experiment. Types of design include repeated measures, independent groups, and matched pairs designs. Note, that the power is indeed much larger for the randomized complete block design.
If you have doubts on that your data violates the assumptions you can always simulate data from a model with similar effects as yours but where are distributional assumptions hold and compare the residual plots. In the most basic form, we assume that we do not have replicateswithin a block. This means that we only observe every treatment once in eachblock. The nuisance factor they are concerned with is "furnace run" since it is known that each furnace run differs from the last and impacts many process parameters.
Matched Pairs Design
You can obtain the 'least squares means' from the estimated parameters from the least squares fit of the model. The sequential sums of squares (Seq SS) for block is not the same as the Adj SS. Variable(s) that have affected the results (DV), apart from the IV. A confounding variable could be an extraneous variable that has not been controlled.
Blocking is most commonly used when you have at least one nuisance variable. A nuisance variable is an extraneous variable that is known to affect your outcome variable that you cannot otherwise control for in your experiment design. If nuisance variables are not evenly balanced across your treatment groups then it can be difficult to determine whether a difference in the outcome variable across treatment groups is due to the treatment or the nuisance variable. The objective of the randomized block design is to form groups where participants are similar, and therefore can be compared with each other. The term experimental design refers to a plan for assigning experimental units to treatment conditions. Randomly allocating participants to independent variable conditions means that all participants should have an equal chance of taking part in each condition.
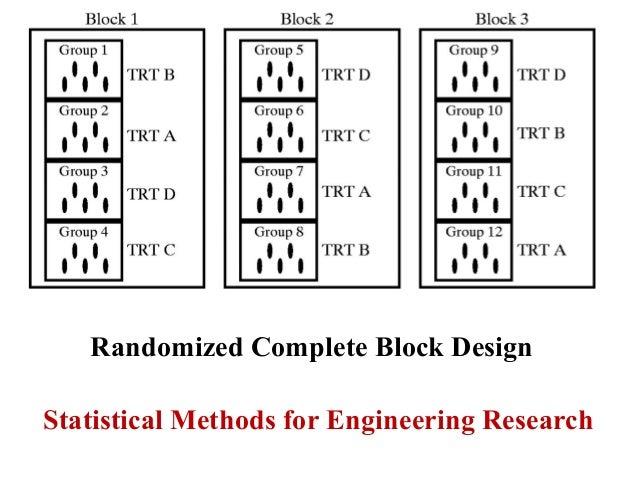
When we can utilize these ideal designs, which have nice simple structure, the analysis is still very simple, and the designs are quite efficient in terms of power and reducing the error variation. A randomized block design is a type of experiment where participants who share certain characteristics are grouped together to form blocks, and then the treatment (or intervention) gets randomly assigned within each block. To address nuisance variables, researchers can employ different methods such as blocking or randomization.
His work in developing analysis of variance (ANOVA) set the groundwork for grouping experimental units to control for extraneous variables. A randomized block design is an experimental design where the experimental units are in groups called blocks. The treatments are randomly allocated to the experimental units inside each block.
Then, the performance outputs of the proposed FF designs were compared under the same conditions assigned in the previous section. The single-cell performance tests yielded that the highest power density was ensured with nickel foam (NF)-serpentine FF with 0.267 W/cm2. This increment corresponds to a 38 % enhancement in the power output when compared to the classical serpentine-type FF.